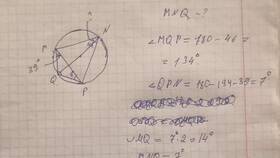Вписанный четырехугольник (четырехугольник, вписанный в окружность) обладает уникальным свойством, касающимся суммы его противоположных углов. Эта особенность является важной теоремой в евклидовой геометрии.
Содержание
Вписанный четырехугольник (четырехугольник, вписанный в окружность) обладает уникальным свойством, касающимся суммы его противоположных углов. Эта особенность является важной теоремой в евклидовой геометрии.
Основная теорема
Для любого вписанного четырехугольника сумма противоположных углов равна 180°. Это свойство можно выразить формулой:
- ∠A + ∠C = 180°
- ∠B + ∠D = 180°
Геометрическая иллюстрация
| Углы | Сумма |
| ∠A и ∠C | 180° |
| ∠B и ∠D | 180° |
Доказательство свойства
- Рассмотрим четырехугольник ABCD, вписанный в окружность
- Угол A опирается на дугу BCD
- Угол C опирается на дугу BAD
- Сумма этих дуг составляет полную окружность (360°)
- По теореме о вписанном угле: ∠A = ½◡BCD, ∠C = ½◡BAD
- Следовательно: ∠A + ∠C = ½(◡BCD + ◡BAD) = ½ × 360° = 180°
Практическое применение
- Решение геометрических задач
- Построение вписанных четырехугольников
- Проверка, можно ли четырехугольник вписать в окружность
- Доказательство других геометрических теорем
Обратная теорема
Если в выпуклом четырехугольнике сумма противоположных углов равна 180°, то около него можно описать окружность. Это важный признак вписанного четырехугольника.
