Процентные вычисления являются важным математическим инструментом, применяемым в различных сферах жизни. Рассмотрим основные принципы и методы расчета процентов.
Содержание
Основные понятия
Процент - это сотая доля числа, обозначаемая знаком %. 1% равен 1/100 части целого.
| Обозначение | 1% = 1/100 = 0,01 |
| Пример | 10% = 10/100 = 0,1 |
Основные формулы расчета
Нахождение процента от числа
Формула: (Число × Количество процентов) ÷ 100
Нахождение числа по его проценту
Формула: (Значение процента × 100) ÷ Количество процентов
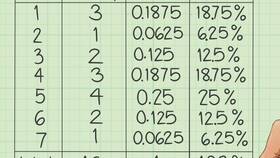
Нахождение процентного соотношения
Формула: (Часть × 100) ÷ Целое
Примеры расчетов
| Тип расчета | Пример | Решение |
| Процент от числа | 15% от 200 | (200 × 15) ÷ 100 = 30 |
| Число по проценту | Число, где 25% = 50 | (50 × 100) ÷ 25 = 200 |
| Процентное соотношение | 30 от 150 | (30 × 100) ÷ 150 = 20% |
Расчет изменения в процентах
Формула для определения процентного изменения:
((Новое значение - Старое значение) ÷ Старое значение) × 100%
- Если результат положительный - увеличение
- Если результат отрицательный - уменьшение
Пример:
Цена выросла с 200 до 250 рублей:
((250 - 200) ÷ 200) × 100 = 25% увеличение
Сложные проценты
Формула сложных процентов:
Итоговая сумма = Начальная сумма × (1 + Процентная ставка)Количество периодов
- Определите начальную сумму (P)
- Установите процентную ставку за период (r)
- Определите количество периодов (n)
- Примените формулу
Пример расчета вклада:
10000 рублей под 5% годовых на 3 года:
10000 × (1 + 0,05)3 = 10000 × 1,157625 = 11576,25 руб.
Практические советы
- Для быстрого расчета 10% - разделите число на 10
- Для расчета 5% - найдите 10% и разделите на 2
- Для расчета 20% - найдите 10% и умножьте на 2
- Используйте калькулятор для сложных расчетов
Освоив эти методы расчета процентов, вы сможете легко решать финансовые и математические задачи в повседневной жизни и профессиональной деятельности.